元のプログラムをソースプログラム、 翻訳の結果と得られるプログラムをオブジェクトプログラムと呼ぶ。 機械語で直接、計算機上で実行できるプログラム を実行プログラムと呼ぶ。オブジェクトプログラムがアセンブリプログラムの 場合には、アセンブラにより機械語に翻訳されて、実行プログラムを得る。他 の言語の場合には、オブジェクトプログラムの言語のコンパイラでコンパイル することにより、実行プログラムが得られる。仮想マシンコードの場合には、 オブジェクトコードはその仮想マシンにより、インタプリトされて実行される。
コンパイラにしてもインタプリターにしても、その構成は多くの共通部分を持 つ。すなわち、ソースプログラムの言語の意味を解釈する部分は共通である。 インタプリターは、解釈した意味の動作をその場で実行するのに対し、コンパ イラではその意味の動作を行うコードを出力する。
言語処理系は、大きく分けて、次のような部分からなる。
コンパイラの性能とは、如何に効率のよいオブジェクトコードを出力できるか であり、最適化でどのような変換ができるかによる。インタープリタでは、プ ログラムを実行するたびに、字句解析、構文解析を行うために、実行速度はコ ンパイラの方が高速である。もちろん、機械語に翻訳するコンパイラの場合に は直接機械語で実行されるために高速であるが、コンパイラでは中間コードで やるべき操作の全体を解析することができるため、高速化が可能である。
また、中間言語として、都合のよい中間コードを用いると、いろいろな言語か ら中間言語への変換プログラムを作ることで、それぞれの言語に対応したコン パイラを作ることができる。
さて、例として最も簡単な数式の評価について、インタプリターとコンパイラ を作ってみることにする。目的は,
の式の入力に対し、この式を計算し、12 + 3 - 4
と出力するプログラムを作ることである。これは、式という「プログラミング 言語」を処理する言語処理系である。「式」という言語では、tokenとして、 数字と"+"や"-"といった演算子がある。11
まずは、字句解析ではこれらのトークンを認識する。例えば、上の例では、
12の数字、+の演算子、3の数字、−の演算子、4の数字、終わりという列に変換する。
tokenは、tokenの種類と12の数字という場合の12の値の2つの組で表される。 以下にtokenの種類を定義するexprParser.hを示す。
字句解析を行う関数getTokenを示す。
exprParser.h (一部) (ソースコードはこちらから)
この関数は、字句を読み込み、currentTokenにtokenの種類、NUMの場合に tokenValに値を返す。 これを使うことにより、いわゆる構文解析しなくても、直接実行する(計算し てしまう)インタプリターは簡単にできる。その動作は以下のような動作であ る。
void getToken() { int c,n; again: c = getc(stdin); switch(c){ case '+': currentToken = PLUS_OP; return; case '-': currentToken = MINUS_OP; return; case '\n': currentToken = EOL; return; } if(isspace(c)) goto again; if(isdigit(c)){ n = 0; do { n = n*10 + c - '0'; c = getc(stdin); } while(isdigit(c)); ungetc(c,stdin); tokenVal = n; currentToken = NUM; return; } fprintf(stderr,"bad char '%c'\n",c); exit(1); }getToken.c (ソースコードはこちらから)
cal.c main() { int t; int op; int result; op = NUM; result = 0; while(1){ getToken() switch(currentToken){ case NUM: switch(op){ case NUM: result = tokenVal; break; case PLUS_OP: result = result + tokenVal; break; case MINUS_OP: result = result - tokenVal; break; } break; case PLUS_OP: case MINUS_OP: op = t; break; case EOL: printf("result = %d\n",result); exit(0); } } }
では、この「式」というプログラミング言語の構文とはどのようなものであろうか。例えば、次のような規則が構文である。
このような記述を、BNF (Backus Naur Form または Buckus Normal Form) という。
このような構造を反映するデータ構造を作るのが、構文解析である。図に示す。
構文解析のデータ構造は、以下のような構造体を作る。これをexprParser.hに 定義しておく。
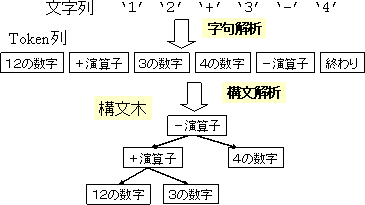
この構文木を作るプログラムが、readExpr.cである。 このプログラムでは、exprParser.hで定義されて いるASTを使って、構文木を作っている。このデータ構造は 式の場合は、演算子とその左辺の式と右辺の式を持つ。数字の場合はこれらを 使わずに値のみを格納する。tokenを読むたびに、データ構造を作っている。
exprParser.h (一部) (ソースコードはこちらから) typedef struct _AST { int op; int val; struct _AST *left; struct _AST *right; } AST; AST *readExpr(void);
readExpr.c (ソースコードはこちらから) AST *readExpr() { int t; AST *e,*ee; e = readNum(); while(currentToken == PLUS_OP || currentToken == MINUS_OP){ ee = (AST *)malloc(sizeof(AST)); ee->op = currentToken; getToken(); ee->left = e; ee->right = readNum(); e = ee; } return e; } AST *readNum() { AST *e; if(currentToken == NUM){ e = (AST *)malloc(sizeof(AST)); e->op = NUM; e->val = tokenVal; getToken(); return e; } else { fprintf(stderr,"bad expression: NUM expected\n"); exit(1); } }
この構文木を解釈して実行する、すなわちインタプリターをつくってみること にする。その動作は、
evalExpr.c (ソースコードはこちらから) int evalExpr(AST *e) { switch(e->op){ case NUM: return e->val; case PLUS_OP: return evalExpr(e->left)+evalExpr(e->right); case MINUS_OP: return evalExpr(e->left)-evalExpr(e->right); default: fprintf(stderr,"evalExpr: bad expression\n"); exit(1); } }
mainプログラムでは、関数readExprを呼び、構文木を作り、それを関数 evalExprで解釈実行して、その結果を出力する。これが、インタプリターであ る。先のプログラムと大きく違うのは、式の意味を表す構文木が内部に生成さ れていることである。この構文木の意味を解釈するのがインタプリターである。 (readExprでは1つだけ先読みが必要であるので、getTokenを呼び出している)
interpreter.c (ソースコードはこちらから) int main() { AST *e; getToken(); e = readExpr(); if(currentToken != EOL){ printf("error: EOL expected\n"); exit(1); } printf("= %d\n",evalExpr(e)); exit(0); }
次にコンパイラをつくってみる。コンパイラとは、解釈実行する代わりに、実 行すべきコード列に変換するプログラムである。実行すべきコード列は、通常、 アセンブリ言語(機械語)であるが、そのほかのコードでもよい。中間コード として、スタックマシンのコードを仮定することにする。スタックマシンは以 下のコードを持つことにする。
コンパイラは、このスタックマシンのコードを使って、式を実行するコード列 を作る。例えば、図で示した例の式12+3-4は下のようなコードになる。
スタックマシンでの実行は以下のように行われる。
stackCode.hには、コードとその列を格納する領域を定義してある。
stackCode.h (ソースコードはこちらから) #define PUSH 0 #define ADD 1 #define SUB 2 #define PRINT 3 #define MAX_CODE 100 typedef struct _code { int opcode; int operand; } Code; extern Code Codes[MAX_CODE]; extern int nCode;
コンパイルの手順は、以下のようになる。
compileExpr.c (ソースコードはこちらから) void compileExpr(AST *e) { switch(e->op){ case NUM: Codes[nCode].opcode = PUSH; Codes[nCode].operand = e->val; break; case PLUS_OP: compileExpr(e->left); compileExpr(e->right); Codes[nCode].opcode = ADD; break; case MINUS_OP: compileExpr(e->left); compileExpr(e->right); Codes[nCode].opcode = SUB; break; } ++nCode; }
コード生成では、ここではスタックマシンのコードをCに直して出力すること にしよう。Cで実行させるために、mainにいれておくことにする。このプログ ラムが、codeGen.cである。
codeGen.c (ソースコードはこちらから) void codeGen() { int i; printf("int stack[100]; \nmain(){ int sp = 0; \n"); for(i = 0; i < nCode; i++){ switch(Codes[i].opcode){ case PUSH: printf("stack[sp++]=%d;\n",Codes[i].operand); break; case ADD: printf("sp--; stack[sp-1] += stack[sp];\n"); break; case SUB: printf("sp--; stack[sp-1] -= stack[sp];\n"); break; case PRINT: printf("printf(\"%%d\\n\",stack[--sp]);\n"); break; } } printf("}\n"); }
コンパイラのmainプログラムであるが、readExprまではインタープリタと同じ である。標準出力に出力されるプログラムに適当に名前をつけ(たとえば、 output.c)これをCコンパイラでコンパイルして実行すればよい。(assembler のファイルの場合はasコマンドでコンパイルする。)
codeGen.c (ソースコードはこちらから) int main() { AST *e; getToken(); e = readExpr(); if(currentToken != EOL){ printf("error: EOL expected\n"); exit(1); } nCode = 0; compileExpr(e); Codes[nCode++].opcode = PRINT; codeGen(); exit(0); }
電卓のプログラムに比べて、構文木を作るなど、ずいぶん遠周りをしたようで あるが、その理由は演算の優先度や、括弧の式など、通常の数学で使われる式 を正しく処理するためである。例えば、
の場合には、掛け算を最初にして、それらを加算しなくてはならない。この処 理を反映した構文木を作ることによって、正しく処理する「言語処理系」を作 ることができるようになる。12*3 + 3*4
% cc -o interpreter interpreter.c evalExpr.c getToken.c readExpr.c
% ./interpreter < input
% cc -o compile compile.c compileExpr.c codeGen.c getToken.c readExpr.c
% ./compile < input > output.c
% cc output.c
% a.out